
- GEOMETRIC AND ARITHMETIC SEQUENCES EQUATIONS HOW TO
- GEOMETRIC AND ARITHMETIC SEQUENCES EQUATIONS SERIES
Use the following formula to compute the sum of arithmetic sequence: Now, let us see what are some of the formulae related to the arithmetic sequence.įormula for Finding the Sum of the Arithmetic Sequence In the above sequence, the difference between the successor and predecessor is -4. Since this constant is positive, so we can say that the arithmetic sequence is increasing. This constant 3 is known as common difference (d). You can see in the above example that each next term is obtained by adding a fixed number 3 to the previous term. If an arithmetic sequence is decreasing, then the common difference is negative.If an arithmetic sequence is increasing, the common difference is positive.We can have an increasing or decreasing arithmetic sequence. All you have to do is to add the common difference in the term to get the next term. This common difference also helps to determine the next term in the sequence. This difference is termed as common difference and is represented by d.

Arithmetic progression is another name given to the arithmetic sequence. An arithmetic sequence means the numbers arranged in such a way that the difference between two consecutive terms is the same.
GEOMETRIC AND ARITHMETIC SEQUENCES EQUATIONS SERIES
When a series of numbers are arranged in a specific pattern, we call it a sequence. We will specifically discuss the following sequences and their formulas: In this article, we have compiled a list of all the formulae related to the series and sequences.
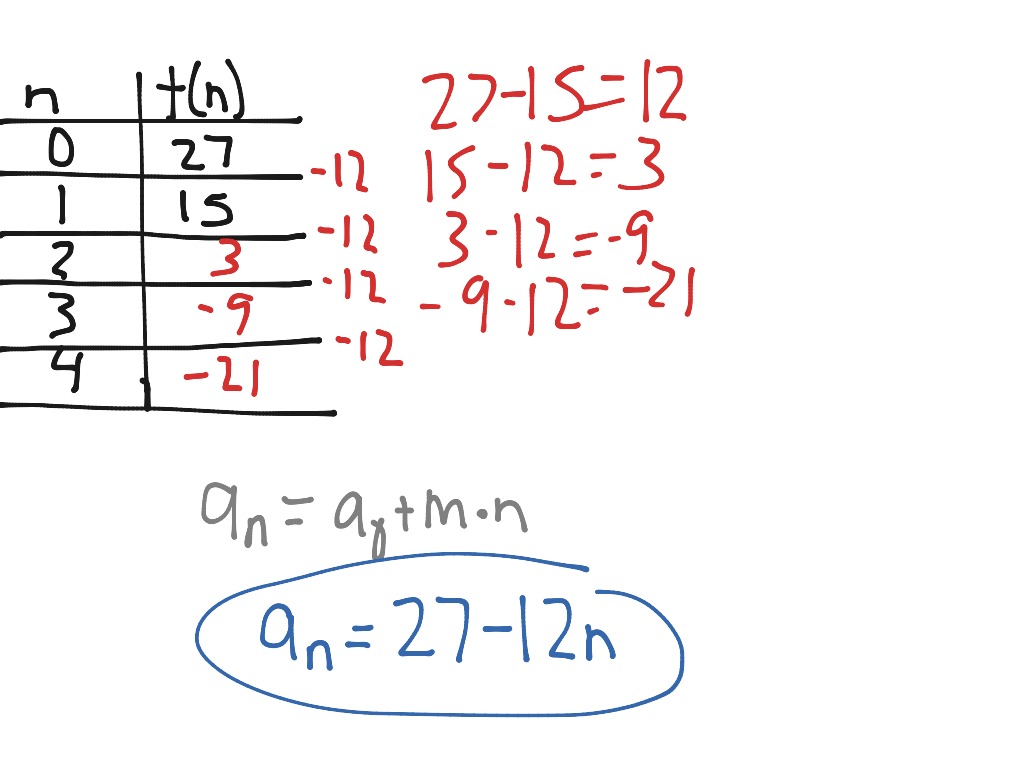
Although sequences resemble sets, however, the main difference between the sets and sequences is that in a sequence, the numbers can occur repeatedly. These series and sequences can be better comprehended by understanding the relevant formulas.

"The sum of all the terms in the sequence is known as series" There is a particular relationship between all terms in the sequence" "A list of numbers arranged in a sequential order. On the other hand, the series represents the sum of all elements in the sequence. A sequence depicts the collection of items in which any kind of repetition is allowed.
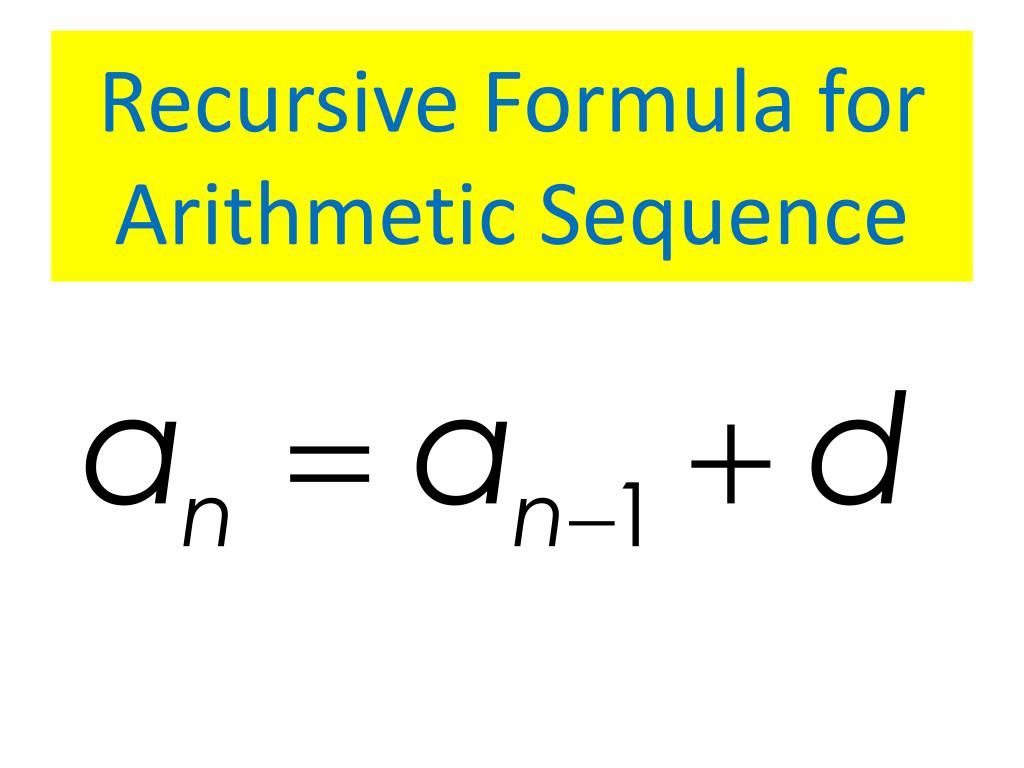
The sequence above shows a geometric sequence where we multiply the previous term by $2$ to find the next term.One of the basic concepts in mathematics is sequences and series. Geometric sequences are sequences where the term of the sequence can be determined by multiplying the previous term with a fixed factor we call the common ratio. So, let’s begin by understanding the definition and conditions of geometric sequences.
GEOMETRIC AND ARITHMETIC SEQUENCES EQUATIONS HOW TO
We’ll also learn how to identify geometric sequences from word problems and apply what we’ve learned to solve and address these problems. We’ll also learn how to apply the geometric sequence’s formulas for finding the next terms and the sum of the sequence. We’ll learn how to identify geometric sequences in this article. Geometric sequences are sequences of numbers where two consecutive terms of the sequence will always share a common ratio. We cab observe these in population growth, interest rates, and even in physics! This is why we understand what geometric sequences are. Geometric sequences are a series of numbers that share a common ratio. Geometric Sequence – Pattern, Formula, and Explanation


 0 kommentar(er)
0 kommentar(er)
